/森羅万象学校
/2004-03-04/
木星の起源:惑星のガス捕獲
生駒 大洋(東工大・理)
mikoma@geo.titech.ac.jp
2004 年 3 月 6 日

|
タイトルぺージ
|

|
本講演の趣旨
|

|
全体目次
|

|
第一部タイトル: 背景と基礎
|

|
太陽系の惑星
- 最近は木星・土星と天王星・海王星をわける
- 木星・土星は gas giant planet と呼ばれる
- 天王星・海王星は ice giant planet と呼ばれる
|

|
木星型惑星の内部構造
- 重力場の観測から密度分布を推定
- 密度分布を説明できるような組成を考える
- 以下では固体核の部分を「コア」と呼ぶ
|

|
木星型惑星の特長
|

|
太陽系形成標準モデル
- 通称「京都モデル」
- 星雲ガスの散逸機構はあまりよくわかっていない
|

|
星雲ガスに埋もれた原始惑星
|

|
大気を持つ条件
- 大気とは「コアの重力によって束縛されたガス」
- ボンディ半径よりも内側を大気と呼ぶ
-
|

|
大気を持つ条件: 木星軌道における場合
- 温度は太陽の放射によって決まる温度(輝度の 1/4 乗に比例)
- 木星軌道では, コアが月ぐらいの大きさになると大気を持てるようになる
|
|
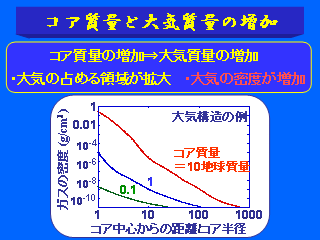
コア質量と大気質量の増加
- コアが成長している途中での, 大気構造の計算例
- 温度は放射と対流によって決まるとする
|

|
高密度大気の自己重力
- 深部の高密度大気による重力も無視できない
- 地球型惑星ではコアからの重力だけを考える
|
|
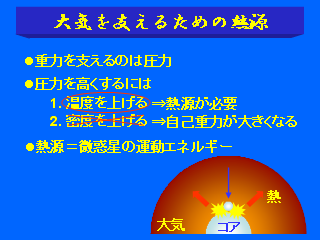
大気を支えるための熱源
- 圧力を高めるために密度を上げるのはダメ
- 熱源は衝突する微惑星の運動エネルギー
- コアの質量も増加することに注意
- 深部での加熱はボンディ半径の大きさには影響しない
|

|
大気の自己重力不安定:
基本的な考え方
|

|
大気の自己重力不安定:
臨界コア質量を越えた場合のプロセス
- 恒星の進化との違いは微惑星の有無: 恒星の場合は初めからガスが収縮
- 木星自体は冷却していると仮定
|

|
木星形成モデル(水野モデル)
- 英語で Mizuno Model とは呼ばれていない
- 恒星進化における暴走的ガス捕獲は gas instability と呼ばれる
|

|
臨界コア質量の制約条件: 現在のコア質量
|

|
臨界コア質量の制約条件: 星雲ガスの寿命
|

|
ここでの「木星を作る」の定義
- 項目 2 の趣旨は, 「現在のコアよりも大きな臨界コアをつくって,
短時間に無理矢理ガスを捕獲して木星を作る,
ということはしない」ということ
|

|
模式図
|

|
役割分担
|

|
これまでの木星形成に関する理解 (1980 年代に確立)
惑星集積理論に不備があると考えられていた
その後理解の変化
- 現在のコア質量は地球質量の 10-30 地球質量かどうかあやしい
- 木星と土星のコアのサイズは異なる
- そもそも臨界コア質量は地球質量の 10-20 倍?
|

|
第一部まとめ
|

|
この後の流れ
|

|
タイトルページ
|

|
惑星モデル
- コア, 大気, 星雲ガスが存在
- 本当に球対称としていいか, 確証はない.
- 地球では大気を薄い平板としてとらえる (球対称としない)
- 大気は定常であるとする
|

|
大気構造を決める(微分)方程式
|

|
基礎方程式: 力の釣合
- 重力: 万有引力
- Mr: 半径 r の内側にある全ての質量
- 分厚い大気を考えているので, 大気の質量も考慮
- 圧力の差で重力を支える
- 釣合の式は静水圧の式になる
|

|
基礎方程式: 圧力と密度の関係
|

|
基礎方程式: 輻射できまる温度
- 2 枚の黒体の板の間の正味の熱フラックス
- 球対称であることを考慮
- 地球のような平行平板: フラックスは一定
- 球対称の場合: フラックスは面積に比例 --> L = 4 πr^2 F
|

|
基礎方程式: 対流できまる温度
- 大気は断熱変化(等エントロピー変化)
- ある高度で熱を解放
- 大気構造はポアソンの関係式でかけるようになる
|

|
基礎方程式: エネルギー収支
- r + Δr と r での差から表現
- 非定常状態では, 大気の収縮膨張に関係する量を追加
|

|
微惑星の運動エネルギー
- エネルギー = 1 g 当たりのエネルギー x 微惑星集積率(単位時間あたりに降って来る量)
|

|
吸光係数
- 吸光係数は温まりやすさの指標
- κL なので, L と同じだけ重要. しかし決め方が難しい
|

|
ダストの吸光係数
|

|
境界条件
- コア半径
- コア半径での熱フラックス
- 外側の星雲ガスと連続(温度, 密度同じ)
|

|
定常解
- 100 万年で地球質量が微惑星によって集積するとしたときの計算
- コアの質量は与える
- 灰色大気だけど, シリケイト, 氷が含まれる. そのため構造がカクカクする
|

|
定常解: 大気質量の増加
- コアの質量増加 -> 大気質量増加
- 10 地球質量以上では定常解がなくなる
- 定常解がなくなる限界コア質量 = 臨界コア質量
|
|
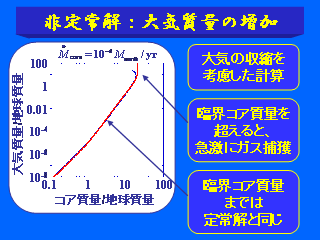
非定常解: 大気質量の増加
- 大気の収縮による熱の発生を考慮
- パラメタは定常解と同じ
- 臨界コア質量を越えると急激にガス捕獲
- 臨界コア質量になるまでは定常解と同じ
|

|
非定常解: 熱フラックス
- 臨界コア質量で熱供給のメカニズムが異なる
- ルミノシティは結果として求まる
|

|
まとめ
- 臨界コア質量: 熱的に定常状態でいられるぎりぎりのコア質量
|

|
この後の流れ
|

|
タイトル
|

|
内容
- 微惑星集積率と吸光係数で臨界コア質量がどう変化するか?
|

|
微惑星集積率と限界コア質量
- 今までは 10^-6. 今回は 10^-5, 10^-7 でも計算
- 集積率が大きいとスケールハイトが大きい
- 大気質量を与えた場合の計算
|

|
微惑星集積率と限界コア質量
- 集積率が大きいと臨界コアは大きくなる
- 依存性はそれほど大きくない
|

|
臨界質量に早く到達したい
- 微惑星集積率を上げる
- 熱の供給を止める -> 大気は収縮するしかない = 臨界コア
|

|
微惑星集積率をあげても
- 制約にうまく合わない
- 現在のコアは 10 倍の地球質量
- 1000 万年で星雲ガス消失
|

|
微惑星集積率を途中で止めても
- 微惑星集積を止めるとすぐにガス収縮. 大気が自分で冷えて熱を供給
- 余計に時間がかかる
|

|
大気質量の増加
- 微惑星収縮を止めてからの時間進化を切り出して見る
- フェーズが 3 つ存在
|

|
熱を捨ててガス捕獲
- 熱が逃げていくことが問題
- エネルギー保存式
- 重力エネルギーと熱エネルギーの時間変化が逃げる熱フラックス
- ガス捕獲時間が見積もれる. 効率的に熱を捨てれるか
|

|
熱フラックスの変化
- 微惑星の集積を止めたことでエネルギー供給が切れる
- 加熱源がなくなるために, その温度構造を保てなくなり急激に冷える
- 大気のスケールハイトが縮む分, 周囲のガスを取り込み, 急激にガス質量が増える
- ある程度温度が下がると, 大気がゆっくりと縮みながら周囲のガスを取り込む
- 解放される重力エネルギーは惑星半径程度なので, 出す熱フラックスも小さい
- ガスの質量が大きくなると自己重力が大きくなり, 暴走的に成長
|

|
臨界エネルギーフラックス
- コアに対して最低限必要な熱フラックス = 臨界熱フラックス
|

|
コア質量とガス捕獲時間との関係
- コアが小さくなるとガス捕獲時間は急激に長くなる
- やっぱり途中で止めてもダメ
|

|
ダストに頼る
|

|
「大気のダストは少ない」という意見
|

|
「大気のダストは多い」という意見
|

|
大気中のダストの吸光係数
- ダストの性質はよくわからない
- 適当なパラメタ f を用いたパラメタライズを用いる
|
|
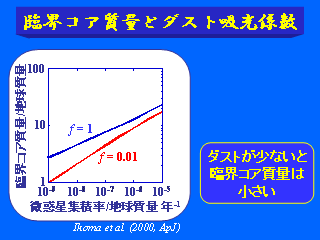
臨界コア質量とダスト吸光係数
- 輻射が卓越するような領域で吸収係数を小さくする
- 温度によって吸収物質が異なることを想定
|

|
臨界コアの形成時間
|

|
ここまでのまとめ
|

|
この後の流れ
|

|
タイトル
|

|
内容
|

|
話しの流れ
|

|
コアの暴走的成長
- 秩序的成長
- 暴走的成長
- 1 つのものが周囲のものを食い尽くす
- 重力で引き付けて成長
|

|
暴走的成長の頭打ち
- 重力的に周囲の微惑星を振り回す -> なかなか微惑星が捕まらない
- 地球質量のコアの成長時間 = 4000 万年
- 暴走成長では成長が頭打ちになり, 時間がかかりすぎる
|

|
微惑星を壊す
- 微惑星同士の衝突 -> 破壊
- 小さい天体ほどガスの抵抗を受ける
-> ランダム運動が押えられる
-> 暴走的成長の頭打ちを回避できる?
|

|
微惑星を増やす: なぜ?
- 林モデル
- 現在の太陽系の元素組成, 存在量によって, 昔の太陽系を再現
- 最小質量星雲モデル
- 0.1 地球質量集積するのでも 1000 万年かかる
|

|
微惑星を増やす: どれくらい?
- 観測による星雲質量の頻度分布
-> 0.001 -- 0.1 Solar
- 林モデル 0.01 Solar
- 本研究では 0.1 Solar
|

|
破片は太陽にも落ちる
- 破片と星雲ガスの摩擦
- 摩擦によりケプラー回転からずれる
- 微惑星を壊し, さらに太陽へ落ちるまえにコアへ集積させる
|

|
破壊を考慮した場合のコア形成
- 図の縦軸は累積の質量.
- 100 万年もたつと, 80 % が太陽へ落ちる.
20 % でコアが作られた.
|
|
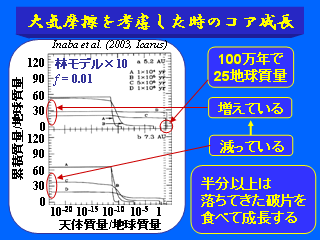
破壊を考慮した場合のコア形成
- 林モデルの 10 倍にした時 -> 赤印(括弧内は太陽からの距離)
- 破片はほとんど太陽へ落下
- 破壊を考慮し, 太陽への落下だけ考慮した場合には説明できない.
|

|
大気による微惑星の捕獲
- 破壊した場合に他の効果は無いか?
- 大気の構造を仮定し, 軌道計算. 重力場から逃げられるか調べた
- 大気の効果で, コアに集積されるようになる
|

|
大気摩擦を考慮した時のコア成長
- 林モデルの 10 倍
- 圧倒的に早くコア集積が生じる
- 図 a の C, D を比べると増えている. 外側から落ちてきたものを集積したことを示す.
|

|
大気摩擦を考慮した時のコア成長
- 大気の捕獲の効果を考慮すると, 臨界コア質量に到達する
- 林モデルの 5 倍程度を考えると良さそう.
-> 他の効果を入れたら林モデルの 1 倍程度になる?
|

|
氷微惑星による大気汚染
- 微惑星は大気中を透過してコアまで到達できない.
- 水素・ヘリウム大気 --> 炭素・酸素大気に
|
|
大気汚染の効果
- 大気中の重元素が増加
-> 平均分子量増加
-> 臨界コアは小さくなる
- CO2 等が入るので吸光係数が大きくなる
-> 臨界コアは大きくなる
|

|
現在の重元素量
- 観測に基づく理論的予測
- 全重元素量 > コア質量
- エンベロープを重元素リッチにしても OK.
|

|
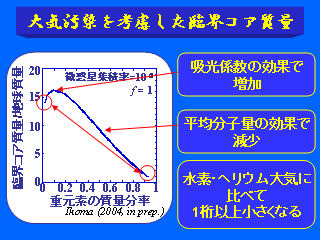
大気汚染を考慮した臨界コア質量
- 重元素量を増やすと....
- 始めは吸光係数の効果で臨界コア質量が増加
- その後は平均分子量の効果で臨界コア質量が減少
-
|
|
大気汚染によるガス捕獲時間の短縮
- 重元素の効果でガスの集積にかかる時間が短縮される
- 暴走成長が始まるまでの捕獲時間
|

|
臨界状態での大気質量
- 臨界状態では大気質量とコア質量の比がほぼ一定
- 赤線はある状態からガス捕獲を開始したときの
重元素比および大気質量の変化を示す
- 星雲ガスは水素ヘリウムなので, 重元素の多い大気は薄まる
|

|
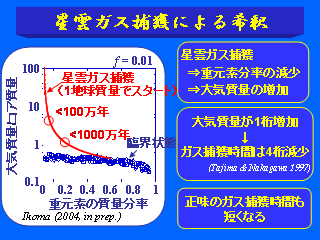
星雲ガス捕獲による希釈
- 大気の質量が 1 桁増えると, ガスの捕獲時間は 4 桁減少
- 正味のガス捕獲時間も早くなる
|

|
大気汚染による形成条件の緩和
- 重元素分率が高ければ林モデルの 3 倍程度でも木星が形成できる
|
|
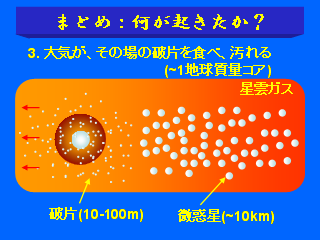
まとめ: 何が起きたか
|

|
まとめ: 何が起きたか
|

|
まとめ: 何が起きたか
|

|
まとめ: 何が起きたか
|

|
まとめ: 何が起きたか
|

|
議題
- なんで地球は木星にならないのか
- 微惑星の破片がたくさん落ちて来るはずでは.
- それを取り込んで臨界質量に達する可能性は?
- 土星問題
- 木星はうまく作れたようだけど, 今までの太陽系形成シナリオとの整合性は?
|
参考文献
- Beckwith, S. V. W., and A. I. Sargent, 1996:
Circumstellar disks and the search for neighbouring planetary systems.
Nature, 383, 139-144.
- Ikoma, M., K. Nakazawa, and H. Emori, 2000:
Formation of giant planets: dependences on core accretion rate and grain
opacity.
ApJ, 537, 1013-1025.
- Inaba, S., G. W. Wetherill, and M. Ikoma, 2003:
Formation of gas giant planets: core accretion models with fragmentation
and planetary envelope.
Icarus, 166, 46-62.
- Inaba, S. and M. Ikoma, 2003:
Enhanced collisional growth of a protoplanet that has an atmosphere.
A&A, 410, 711-723.
- Podolak, M., 2003:
The contribution of small grains to the opacity of protoplanetary
atmospheres.
Icaurs, 165, 428-437.
- Podolak, M., J. B. Pollack, and R. T. Reynolds, 1988:
Interactions of planetesimals with protoplanetary atmospheres.
Icarus, 73, 163-179.
- Pollack, J. B., D. Hollenbach, S. Beckwith, D. P. Simonelli, T. Roush,
and W. Fong, 1994:
Composition and radiative properties of grains in molecular clouds and
accretion disks.
ApJ, 421, 615-639.
- Tanaka, H., and S. Ida, 1999:
Growth of a migrating protoplanet.
Icaurs, 139, 350-366.
- Wuchterl et al., 2000: Giant planet formation.
in Protostars and planets IV, Arizona Press, 1081-1109.
小高 正嗣 & 杉山 耕一朗 (2004-03-12) © 森羅万象学校企画グループ
|