/地球流体セミナー /講演資料一覧 /2004-09-13/

二次元非発散モデルで得られる極渦の周期的変動

 日尾 泰子(京大・理)
2004 年 9 月 15 日
講演ビデオを見るには, 以下の各スライド画像をクリックし, 左上に表示される「ビデオ開始」をクリックしてください.
タイトルぺージ

成層圏極渦を想定した二次元球面モデル実験
  • 波-波の相互作用を想定した実験
  • パラメタ走査実験

話題 1: モデル説明と観測と非常に似た結果について

モデル
  • モデルの概略
  • 渦位の式
  • 定在な波数 1 を作るために「山」を置いている
  • 解が定常になるまで積分を続ける

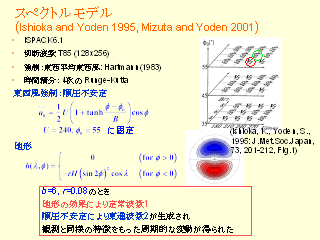
スペクトルモデル
  • 順圧不安定な基本場を作るような東西風強制
  • パラメータ
    • r: 地形の高さ
    • b: ジェットの幅
  • B=6, r=0.08 というパラメタは山が無ければ, 東西波数 2 の定常な解が得られる.

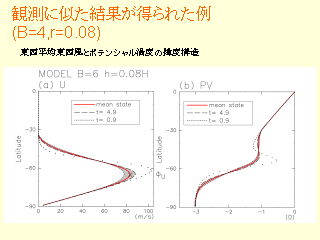
観測と似た結果が得られた例
  • 似ているところ
    • U の最大値, 最大振幅の高さ
    • PV フラットになっている高さ

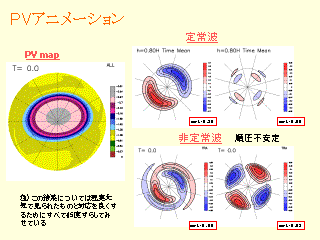
PV アニメーション
  • 波数, 1,2 ともに東進
  • 波数 1 ? 節構造
  • 順圧不安定 + 山の効果
  • PV コンター: 「ぶよぶよ」しながら東進.
    観測よりも波数 2 が小さい印象だが, 十分似ていると言える.
  • 非定在波: 振幅を変えながら東進

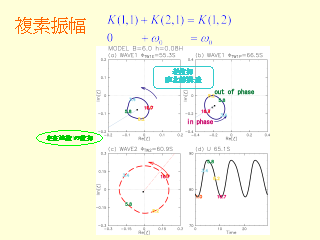
複素振幅
  • 波数 1,2 ともに東進, 逆位相, ... の様子が観測と類似
  • 周期変動なので, 赤の日付同士と青の日付同士は重なり合っている

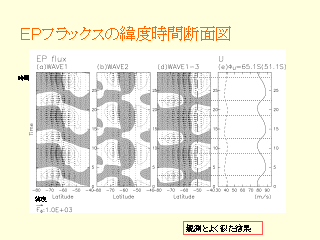
E-P フラックスの緯度時間断面図
  • 波数 1,2 ともに　-60 度が節. 時間とともに正負を変える, 観測と一致
  • 基本的に波数 1 による E-P フラックスによって風速が変化

エンストロフィー式による診断
  • 「波と波の相互作用」を診断したい
  • 伝統的にエンストロフィーを利用する

Smith et al 1984
  • 北半球の突然昇温の際のデータ解析
  • 空間構造は見ていない

エンストロフィー式の導出 (1)
  • 支配方程式(渦度の式)を東西方向にフーリエ展開

エンストロフィー式の導出 (2)
  • 波数 k 成分の式に, 線形の式には存在しなかった波数同士の相互作用が現れる.
  • (4)式の右辺第 3 項には ik (複素数)がかかるのでは?

エンストロフィー式の導出 (3)
  • 複素量((4)式の右辺第 3 項)を無くするために q^bar, q_k をかけ算する
  • 波数 k 成分の式に波数同士の相互作用が現れる.

b=6 エンストロフィー式のバランス関係: 帯状成分
  • 順圧不安定な強制は波の相互作用とキャンセルアウト
  • ぱっと見キャンセルアウトするように見えないかもしれないが, 足しあわせればちゃんと 0 となる.
  • r を大きくする(山を高くする)と波数 1 との相互作用が卓越する

b=6 エンストロフィー式のバランス関係: 波数 2 成分

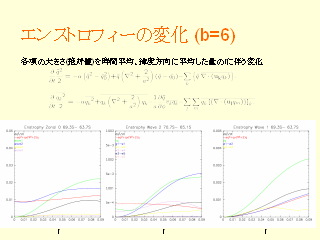
エンストロフィーの変化 (b=6)
  • r を大きくした時の各項の大きさ
  • 山を大きくすると

エンストロフィーによる診断
  • (5)式, (6)式の各項について絵を書いてみる
  • 上から2 段目, 左から 3 枚目 (波-平均平均相互作用) で大体説明できる
    • -60 度が節. 時間とともに正負を変える
  • 上から2 段目, 左から 4 枚目 (波-波平均相互作用, 波数1) の振幅も大きい

まとめ

話題 2: パラメタ走査実験

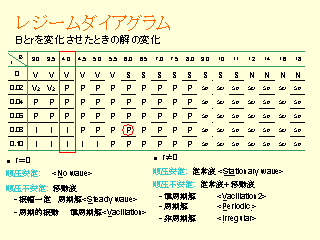
レジームダイアグラム
  • ジェットの幅と山の高さを変化させた時の解の変化
  • r=0.08, b=6 のパラメタレンジでは波数 2 な波が立つ
この研究では b=4 の時について詳細に見ていく. b=4.0 とし r を変化させる.

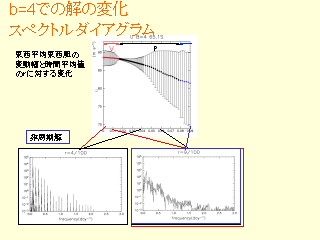
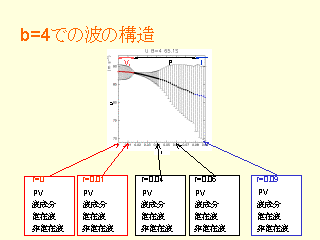
b=4 での解の変化: スペクトルダイアグラム
  • r を大きくしていくと一度小さくなった振幅が再び増大
  • 実は V2 に分類される準周期解が存在する
    • Ishioka ダイヤグラムでは刻み幅が大きすぎて現れていない

b=4 での波の構造

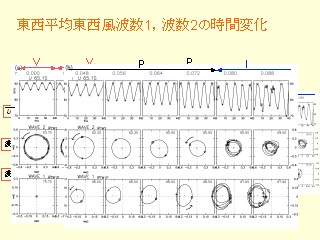
b=4 での平均東西風, 波数 1, 波数 2 の振幅の変化
  • 波数 2: 一旦 steady な状態になってから再び振幅が増大
    • 順圧不安定な forcing をあたえているのに....

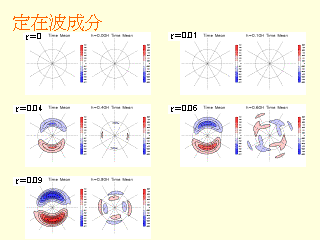
定在波成分

東西平均東西風の波数 1, 波数 2 の時間変化
  • r を増やした際の変化
  • 波数 2 の振幅は大きく
  • 波数 1 の振幅は小さく, 楕円に近付く

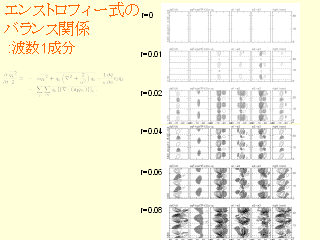
エンストロフィー式のバランス関係: 帯状成分
  • 始めは波数 2 が卓越する
  • r=0.02 で振幅が 0 に近付く
  • あるところから波数 1 によって帯状なものの変動が引き起こされるようになる
  • r = 0.06 までは, 山が風に当たる効果, w2-w3

エンストロフィー式のバランス関係: 波数 2 成分
  • r=0.08 以降では, w1-w1 の寄与が最も大きそうである
  • r=0.06 までは波数 2 の寄与が大きい

エンストロフィー式のバランス関係: 波数 1 成分

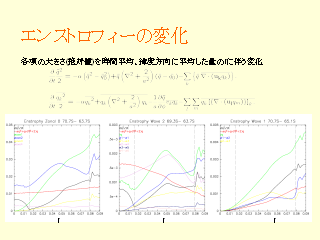
エンストロフィーの変化
  • エンストロフィーの各項の大きさの変化
  • 同じ周期解 (0.02--0.06) であっても各項の寄与が違う
  • 寄与の大きな波数が途中で変わる
  • 山が小さい --> 波数 2 が支配的. 波数 2 が砕波して波数 4 に
  • 山が小さい --> 波数 2 が支配的.

エンストロフィーの変化 (b=6)

おまけ: 主成分解析
  • 主成分分析の練習問題
  • (a) 振幅一定の移動波
    • EOF1, EOF2 は 50 % ずつ
    • PC1-PC2 係図は円になる
  • (b) 周期変動する移動波
    • EOF1=55% , EOF2=55 %
    • PC1-PC2 図は楕円になる
  • 2ω の部分を ω にすると円で右にずれる
  • 3ω にするとおにぎり型になる

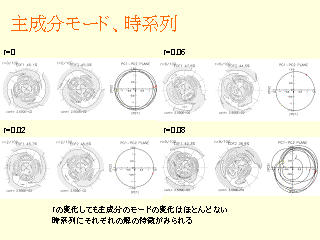
主成分モード, 時系列
  • r=0 は, 練習問題 (c) に似ている
  • 波数 2 の成分しかないように見える

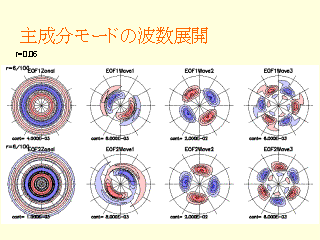
主成分モードの波数展開
  • モデルの EOF1, EOF2 の結果について, 波数展開した
  • これまで述べてきた構造の特徴とよく一致する
    • wave1:
      • EOF1, EOF2 の位相は 90 度ずれている
      • EOF2 の特徴的な構造
      • EOF1, EOF2 の節のある構造
    • wave2:
      • EOF1, EOF2 の位相は 45 度ずれている
    • zonal:
      • モードの構造
  • r を変えた時の EOF はどうなるのか ?
  • 波数展開したのちに, EOF をかけてみるとよいのではないか ?

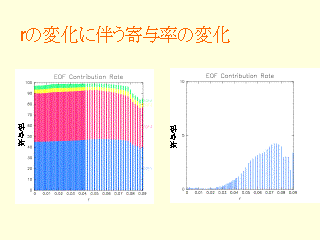
r の変化に伴う寄与率の変化

Real World への応用
  • 練習問題を踏まえて….

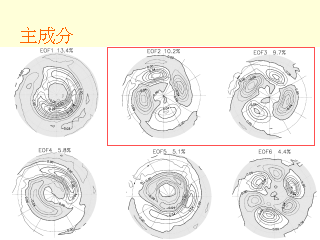
主成分
  • EOF により取り出した構造
  • 波数 1 の振幅が大きいと極渦は弱まる

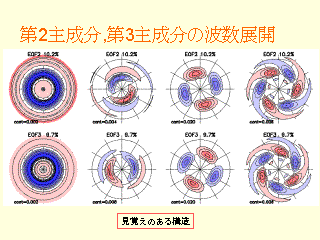
第 2 主成分, 第 3 主成分の波数展開
  • EOF の後, 波数展開をした
  • 3 ヶ月分のデータを使っている
  • 季節進行の成分が入り, 寄与率が低くなっている ?
  • それぞれの波数における EOF1, EOF2 は直交していない

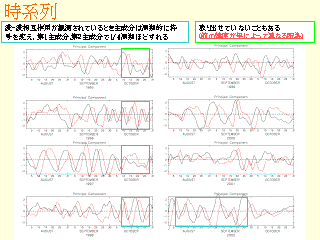
時系列
  • 1996, 1998 年の典型例では EOF で特徴的な構造が取り出せる
  • うまく取り出せない場合もある
  • 恣意的に取り出すのではなく, なんらかの条件で時系列を取り出せるようにしたい

まとめ

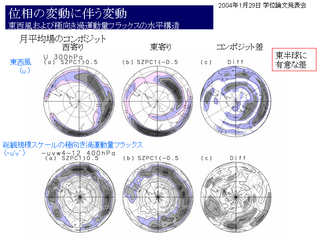
位相の変動に伴う変動

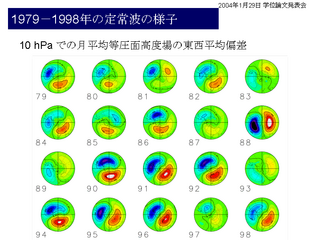
1979--1998 年の定常波の様子

参考文献
  • Ishioka, K., Yoden, S., 1995: Non-linear aspects of barotropically unstable polar vortex in a forced-dissipative system: flow regimes and tracer transport. J. Meteor. Soc. Japan, 73, 201--212.
  • Mizuta, R., Yoden, S., 2001: Chaotic mixing and transport barriers in an idealized stratospheric polar vortex. J. Atmos. Sci., 58, 2615--2628.
  • Hartmann, D.L., 1983: Barotropic instability of the polar night jet stream. J. Atmos. Sci., 40, 817--835
  • Smith, A.K., Gille, J.C., Lyjak, L.V., 1984: Wave-wave interactions in the stratosphere: observations during quiet and active wintertime periods. J. Atmos. Sci., 41, 363--373.
  • Robinson, W.A., 1985: A model of the wave 1-wave 2 vacillation in the winter stratosphere. J. Atmos. Sci., 42, 2289--2304.
  • Scinocca, J.F., Haynes, P.H., 1998: Dynamical forcing of stratospheric planetary waves by tropospheric baroclinic eddies. J. Atmos. Sci., 55, 2361--2392.

SUGIYAMA Ko-ichiro & YAMADA Yukiko 2004-09-22