/地球流体セミナー /講演資料一覧 /2003-09-08/

球面上の渦層の不安定

 坂上 貴之(北大・数学)
2003 年 9 月 10 日
講演ビデオを見るには, 以下の各スライド画像をクリックし, 左上に表示される「ビデオ開始」をクリックしてください.
タイトルぺージ

はじめに: 2 次元の渦層
  • 2 次元の平行流, y = 0 を境に速度が反転するような場合.
  • 速度の飛びがある所でのみ渦度が存在する.
  • Kelvin-Helmhortz 不安定を起こすような設定.

球面上の渦層
  • 設定 : 北緯 30 N の緯度円上でのみ渦度を持つ.

球面の渦層を表す方程式

極渦

考える式

定常解
  • 同じ緯度に渦層があると仮定して解く

線形安定性解析

線形安定性解析 : 固有値
  • ふつうの KH 不安定では, Γ1, Γ2 が 0. 成長率は |n| に比例.

特異性を含む数値計算の方法

特異性が出るまでの時間
  • 2 階微分に特異性が出る. 流れ場, 渦度場は連続に見える.
  • 普通の KH 不安定の場合も同じ.



もっと長い時間計算するには?
  • 特異化パラメータ σ : ある波数より大きい成分を 0 にする. 高周波を落す人工粘性のようなもの.

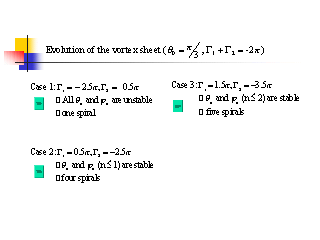
数値計算結果
  • case1: 4 の渦ができる [ムービー]
    • 特異性は渦のない時間帯に現れる.
  • case2: 1 つの渦ができる [ムービー]
  • case3: 5 つの渦ができる [ムービー]

まとめ

おまけ
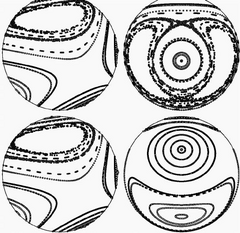
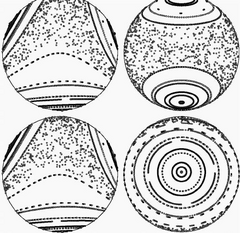
球面上の 3 つの渦点を置いた場合のポアンカレマップ (1)

おまけ
球面上の 3 つの渦点を置いた場合のポアンカレマップ (2)

おまけ
球面上の 3 つの渦点を置いた場合のポアンカレマップ (3)

おまけ
球面上の 3 つの渦点を置いた場合のポアンカレマップ (4)

Odaka Masatsugu 2003-09-10