/地球流体セミナー /講演資料一覧 /2003-09-08/

波の共鳴による不安定の理解
(通常のモードどうし)

 伊賀 啓太(九大・応用力学研究所)
2003 年 9 月 9 日
講演ビデオを見るには, 以下の各スライド画像をクリックし, 左上に表示される「ビデオ開始」をクリックしてください.
タイトルぺージ

はじめに
共鳴を起こす中立モードの特定のしかた
  • 2 つの波のうち片方だけが存在する部分系を考える.
  • 分散曲線, 固有関数の構造を調べ, 不安定波のそれらと比較する.
注意: あらゆる場合に適応できるわけではない.

シアー不安定の部分系解析
  • 片方の波だけ存在する速度分布を考える.

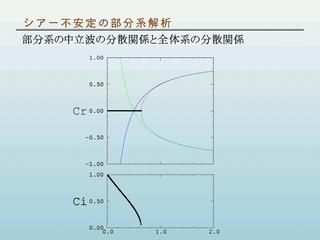
部分系と全体系の分散曲線
  • 緑線 : y = - L で折れる曲がる速度分布の場合
  • 青線 : y = L で折れる曲がる速度分布の場合
  • 黒線 : 全体系の分散曲線
不安定が起こる場所は中立波の分散曲線の交点
  • 不安定の起こる波数領域(cut off)はどう決める ?
    波の構造がわからないと決められない.
  • この場合は低波数側に不安定領域
    • 振幅は exp (-ky) に比例している.
    • 波数の小さいほうが相互作用を起こしやすい.
例題:
dx/dt = -iωxx + αy
dy/dt = -iωyy + βx
固有値 λ は
λ = - i(ωx + ωy)/2 +- [- (ωx - ωy)2/4 + αβ]1/2
αβ > (ωx - ωy)2/4 なら不安定.

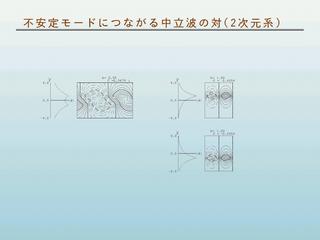
部分系と全体系の波の構造
  • 左 : 全体系の不安定波の構造
  • 右上 : y = - L で折れる曲がる速度分布の場合
  • 右下 : y = L で折れる曲がる速度分布の場合

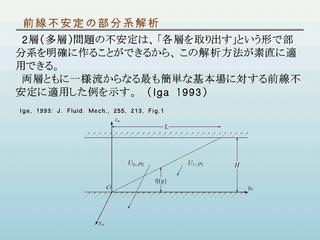
前線不安定の部分系解析 (Iga, 1993)
  • 運動は鉛直に一様
  • ρ1 > ρ2, U1 < U2
  • コリオリ力と圧力がつりあった状態を基本場
部分系の考え方
  • 下側だけ考える: 上側は厚さ無限の層, 速度は 0
  • 上側だけ考える: 下側は厚さ無限の層, 速度は 0

固有値問題の結果 (Orlanski, 1969)

固有値問題の結果 (Iga, 1993)

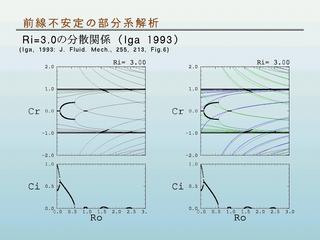
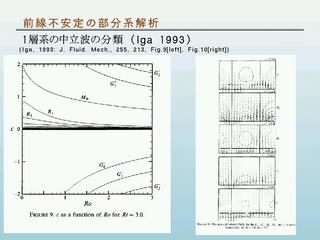
分散関係図 (Iga, 1993)
  • 左 : 全体系
  • 右 : 部分系
    • 緑線 : 下側だけを考えた場合
    • 青線 : 上側だけを考えた場合

部分系の波の構造 (Iga, 1993)
左図は前線面を z から眺めた構造. 上から順に
  • G1+ : 重力波
  • M0 : ケルビン-ロスビー波
  • R1 : ロスビー波
  • G0- : 重力波
  • G1- : 重力波

不安定波の構造との比較 (Iga, 1993)
下層の M0 と上層の R1 との組合せで説明できる.

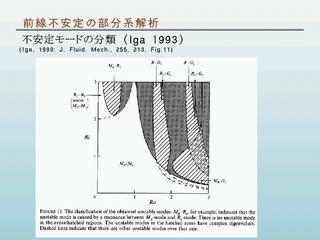
不安定モードの分類図 (Iga, 1993)

部分系が作りにくい場合
  • 不安定モードにつながる中立波をさがす

浅水系, 赤道 β 面モデル (Hayashi and Young, 1987)
  • 1.5 層流体, 下層は静止, 厚さ無限.
  • 上層の渦位が 0 になるように速度場を与える.
  • 上層の厚さは速度場と地衡流バランスするように決める.

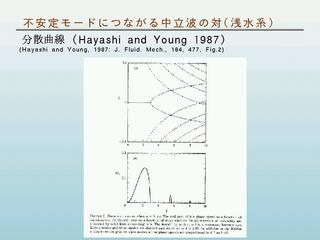
分散曲線 (Hayashi and Young, 1987)
  • k = 5.6 の不安定に注目

不安定波と中立波の構造 (Hayashi and Young, 1987)
  • 上 : 高緯度側に捕捉された中立波
  • 中 : 低緯度側に捕捉された中立波
  • 下 : 不安定波





参考文献
  • Hayashi, Y.-Y., and W. R. Young, 1987: Stable and unstable shear modes on rotating parallel flow in shallow water. J. Fluid. Mech., 184, 477-504.
  • Iga, K., 1993: Reconsideration of Orlanski's instability theory of frontal waves. J. Fluid. Mech., 255, 213-236.
  • Orlanski, I., 1968: Instability of frontal waves. J. Atmos. Sci., 25, 178-200.

Odaka Masatsugu 2003-09-09