平面ポアズイユ流の安定性

概要

2枚の平板に挟まれた流体層を考える． いま，下端境界 $z_*=0$ で温度 $\theta_0$， 上端境界 $z_*=d$ で温度 $\theta_1$ が与えられている． このとき熱伝導解は，流体中で温度が高さとともに線形に変化する， すなわち $\theta(x,y,z)=(\theta_1-\theta_0)/d*z + \theta_0$ である．ここで $d$ は流体層の厚さである． このときに与えた撹乱はある条件で不安定となり， 対流が起こる．これをベナール対流と呼ぶ．

ここで，上下境界においてはrigid(すべりなし条件)とする． このときの流れの安定性を数値的に調べる．

背景

Bénard (1900)の実験において， ベナールは水平方向に六角形のセル状の対流パターンが現れることを見出した． Rayleigh (1916)では上下境界で応力なし条件の線形安定性を調べた． このとき，臨界レイリー数 $Ra=657.5$ となった． これは解析的に陽に求めることができる． 一方，上下境界がrigidの場合には数値的に求めるしかない．

ベナール対流は，線形論による臨界レイリー数/臨界波数と実験結果とが よく一致することから，より精緻な理論を構築することができ， 従ってベナール対流はこれまで非常に詳しく研究されてきた．

ベナール対流は初期条件によって，二次元ロール状対流になったり， 六角形セル状の対流になったりする． しかし，ここでは臨界波数の大きさを求めるまでとし， その向きについては問題にしない．

定式化

基礎方程式は，ブシネスク近似方程式系である． ブシネスク近似方程式系の導出は Chandrasekhar (1961), Drazin and Reid (2004) を参照すること．

基本場 $\Dvect{U}_*$, $\Theta_*$, $P_*$ は， \begin{align} % \Dvect{U}_* &= 0, \\ \Theta_* &= \theta_0 - \beta z_*, \\ P_* &= p_0 - g\rho_0 \left( z_*+\frac{1}{2}\alpha\beta z_*^2 \right). % \end{align} ここで $\beta:=(\theta_0-\theta_1)/d$ とする. $\theta_0 > \theta_1$ つまり $\beta > 0$ の状況を考える.

撹乱についての時間発展方程式

速度ベクトル, 温度, 圧力を基本場とそれからのずれに分けて書くと, \begin{align} % \Dvect{u}_* &= \Dvect{u}_*' ( \Dvect{x}_*, t_* ), \\ \theta_* &= \Theta_* (z_*) + \theta_*' ( \Dvect{x}_*, t_* ), \\ p_* &= P_*(z_*) + p_*' ( \Dvect{x}_*, t_* ) % \end{align} とする.

撹乱についての連続の式，運動方程式，温度の時間発展方程式は， \begin{align} % \nabla_* \cdot \Dvect{u}_* &= 0, \\ % \frac{D u_{*i}}{Dt_*} &= - \frac{\partial}{\partial x_i}\left( \frac{p_*}{\rho_0} + gz_* \right) - \alpha g (\theta_0-\theta_*)\delta_{i3} + \nu\Delta_* u_{*i}, \\ % \frac{D \theta_*}{Dt_*} &= \kappa \Delta_* \theta_*. % \end{align} これに代入して, 摂動に関する方程式を得る: \begin{align} % \nabla_* \cdot \Dvect{u}_*' &= 0, \\ % \frac{D \Dvect{u}_*'}{Dt_*} &= - \nabla_*p_*' + g\alpha\theta_*'\Dvect{k} + \nu\Delta_* \Dvect{u}_*, \\ % \frac{D \theta_*}{Dt_*} &= \frac{D \Theta_*}{Dt_*} +\frac{D \theta_*'}{Dt_*} = -\beta w_*' +\frac{D \theta_*'}{Dt_*} = \kappa \Delta_* \theta_*' % \end{align} となる.

線形化

これを線形化して, \begin{align} % \nabla_* &\cdot \Dvect{u}_*' = 0, \\ % \frac{\partial \Dvect{u}_*'}{\partial t_*} &= - \nabla_*p_*' + \alpha g \theta_*' \Dvect{k} + \nu\Delta_* \Dvect{u}_*, \\ % \frac{\partial \theta_*'}{\partial t_*} &-\beta w_*' = \kappa \Delta_* \theta_*' % \end{align} となる.

無次元化

無次元化を行う． 長さ $L$, 時間 $T$, 速度 $U$, 温度 $\theta$ は, それぞれ $L=[d]$，$T=[d^2/\kappa]$, $\theta=[\beta d]=[\theta_0-\theta_1]$, また， $\frac{U}{T} = \left[ \frac{1}{\rho_0}\nabla p \right] = \frac{1}{L}\left[ \frac{p}{\rho_0} \right]$， $U/T = [ d/(d^2/\kappa)^2]$， 従って，$[p] = [\rho_0]L^2T^{-2}=[\rho_0]\kappa^2/d^2$ なので，無次元化した変数をアスタリスクなしの記号で表して, \begin{align} % \Dvect{x} &= \Dvect{x}_*/d, \\ % t &= \kappa t_*/d^2, \\ % \Dvect{u} &= d\Dvect{u}_*'/\kappa, \\ % \theta &= \theta_*'/(\beta d), \\ % p &= d^2 p_*'/(\rho_0\kappa^2) % \end{align} とする.

方程式を無次元化すると, \begin{align} % \nabla &\cdot \Dvect{u} = 0, \\ % \frac{\partial \Dvect{u}}{\partial t} &= -\nabla p +RPr\theta \Dvect{k} + Pr\Delta\Dvect{u} \\ % \frac{\partial \theta}{\partial t} &- w = \Delta\theta % \end{align} となる. ここで, 二つの無次元数, Rayleigh数 $R$, Prandtl数 $Pr$を \begin{align} % R &:= \frac{g\alpha\beta d^4}{\kappa \nu}, \\ % Pr &:= \frac{\nu}{\kappa} % \end{align} と定義した.

解くべき方程式

渦度方程式を導出する. 運動方程式のローテーションを取る. 渦度$\Dvect{\omega}=\nabla\times\Dvect{u}$を用いて \begin{align} % \frac{\partial \Dvect{\omega}}{\partial t} &= RPr\nabla\times(\theta\Dvect{k})+Pr\Delta\Dvect{\omega} % \end{align} さらに渦度方程式のローテーションを取る. ここで, 次式を用いる: \begin{align} % \nabla\times(\nabla\times\Dvect{u}) &= \epsilon_{lmi}\Dvect{e}_l\partial_m ( \epsilon_{ijk}\partial_j u_k ) \notag \\ &= \epsilon_{ilm}\epsilon_{ijk}\Dvect{e}_l\partial_m\partial_j u_k \notag \\ &= \delta_{jl}\delta_{km}\Dvect{e}_l\partial_m\partial_j u_k -\delta_{jm}\delta_{kl}\Dvect{e}_l\partial_m\partial_j u_k \notag \\ &= \Dvect{e}_j\partial_j \partial_k u_k -\Dvect{e}_k\partial_j^2 u_k \notag \\ &= \nabla(\nabla\cdot\Dvect{u})-\Delta\Dvect{u} \notag \\ &= -\Delta\Dvect{u} % \end{align} ここで恒等式 $\epsilon_{ijk}\epsilon_{ilm}=\delta_{jl}\delta_{km}-\delta_{jm}\delta_{kl}$ を用いた. 同様に, \begin{align} % \nabla\times(\nabla\times(\theta\Dvect{k})) &= \nabla\left(\nabla\cdot(\theta\Dvect{k})\right)-\Delta(\theta\Dvect{k}) = \nabla\left(\frac{\partial\theta}{\partial z}\right) -\Delta\theta\Dvect{k} % \end{align} であるから, \begin{align} % \frac{\partial \Delta \Dvect{u}}{\partial t} &=-RPr\nabla\times(\nabla\times(\theta\Dvect{k})) + Pr\Delta^2 \Dvect{u} \\ &=RPr\left( \Delta\theta\Dvect{k} -\nabla\left( \frac{\partial\theta}{\partial z} \right) \right) +Pr\Delta^2 \Dvect{u} % \end{align} となる.

特に $z$ 方向は \begin{align} % \frac{\partial \Delta w}{\partial t} &=RPr\Delta_1\theta + Pr\Delta^2 w % \end{align} ここで, $\Delta_1 := \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}$ とした. $\theta$ を消去すると, \begin{align} % \left( \frac{1}{Pr}\frac{\partial}{\partial t} - \Delta \right) \Delta w &= R \Delta_1 \theta, \qquad % \left( \frac{\partial}{\partial t} - \Delta \right) \theta = w % \end{align} であるから, \begin{align} % \left( \frac{\partial}{\partial t} - \Delta \right) \left( \frac{1}{Pr}\frac{\partial}{\partial t} - \Delta \right) \Delta w &= R \Delta_1 w % \end{align} となる. あるいは, $w$を消去して, \begin{align} % \left( \frac{\partial}{\partial t} - \Delta \right) \left( \frac{1}{Pr}\frac{\partial}{\partial t} - \Delta \right) \Delta \theta &= R \Delta_1 \theta % \end{align} となる.

連続の式 \begin{align} % \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} &=0 % \end{align} を $x$, $y$ で偏微分することで, \begin{align} % \Delta_1 u &= \frac{\partial}{\partial y} \left( \frac{\partial u}{\partial y} - \frac{\partial v}{\partial x} \right) -\frac{\partial^2 w}{\partial x \partial z} = -\frac{\partial^2 w}{\partial x \partial z} -\frac{\partial \omega_3}{\partial y}, \\ % \Delta_1 v &= \frac{\partial}{\partial x} \left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) -\frac{\partial^2 w}{\partial y \partial z} = -\frac{\partial^2 w}{\partial y \partial z} -\frac{\partial \omega_3}{\partial x} % \end{align} が得られ, $\omega_3$ は渦度方程式の $\Dvect{k}$ 成分の式 \begin{align} % \frac{\partial \omega_3}{\partial t} &= Pr\Delta \omega_3 % \end{align} より与えられる. こうして $\omega_3$, $w$ がそれぞれ求まるので, $u$, $v$ も求めることができる.

境界条件

境界条件としては， $z=0,1$ でrigid, $z=0,1$ において $u=v=w=0$, よって $\omega_3=0$. 連続の式より, $\frac{\partial w}{\partial z}=0$ である. また，温度について \begin{align} % \theta &= 0 \qquad \mbox{at} \quad z=0,1 % \end{align} を課す．

ノーマルモード

支配方程式系は$x$, $y$について対称なので, $s=\sigma+i\omega$として, \begin{align} % w &= W(z)f(x,y)e^{st},\quad \theta = T(z)f(x,y)e^{st} % \end{align} と置いた. \begin{align} % \frac{\partial \theta}{\partial t} -w &= \Delta \theta % \end{align} は, $D:=d/dz$を用いて, \begin{align} % (D^2+\Delta_1-s)Tf = -fW % \end{align} と変形できる. この両辺を$Tf$で割ると, 変数分離形 \begin{align} % \frac{1}{T}D^2T + \frac{W}{T} -s &= -\frac{1}{f}\Delta_1 f =: a^2 % \end{align} に帰着できる. 従って, \begin{align} % \Delta_1 f + a^2 f &= 0,\\ % (D^2-a^2-s)T &= -W % \end{align} となる. また, \begin{align} % \frac{\partial}{\partial t}\Delta w &= RPr\Delta_1\theta+Pr\Delta^2w, \\ % \left(\frac{\partial}{\partial t} -\Delta \right) & \left(\frac{1}{Pr}\frac{\partial}{\partial t} -\Delta \right) \Delta w = R\Delta_1 w % \end{align} は, \begin{align} % (D^2-a^2)(D^2-a^2-s/Pr)W = a^2 RT, \notag \\ % (D^2-a^2-s)(D^2-a^2)(D^2-a^2-s/Pr)W = a^2 RW, % \end{align} となる. 境界条件は, $z=0,1$において, \begin{align} % W&=DW=T=0, \qquad \mbox{rigid} \\ % W&=D^2W=T=0 \qquad \mbox{free} % \end{align} または \begin{align} % W&=DW=T=D^4W-2a^2D^2W-s/PrD^2W=0, \qquad \mbox{rigid} \\ % W&=D^2W=T=D^4W=0 \qquad \mbox{free} % \end{align} となる.

離散化

変数分離によって得られた鉛直構造を表す変数 $W(z)$, $T(z)$に関する方程式を 2次精度有限差分で離散化し，係数行列を求め， 一般化固有値問題を構成する．

具体的には，$W(z_j)$，$T(z_j)$，$(j=0,1\dots,N)$ のあわせて$2(N+1)$個の変数から 境界で既知の値$W(z_0)$，$W(z_N)$，$T(z_0)$，$T(z_N)$の4点を除いた $2(N-1)$個の$W(z_j)$，$T(z_j)$に関する連立一次方程式が， $z_j=j/N$，$(j=0,1\dots,N)$において 成り立つことを要請する．

$a$-$Ra$平面での擾乱の成長率を求める. 支配方程式を行列で書くと, \begin{align} % \left( \begin{array}{cc} Pr(D^2-a^2)^2 & -a^2RPr \\ 1 & D^2-a^2 \end{array} \right) \left( \begin{array}{c} W(z) \\ T(z) \end{array} \right) &= s \left( \begin{array}{cc} D^2-a^2 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{c} W(z) \\ T(z) \end{array} \right) % \end{align} である. これは固有値$s$,固有関数$(W, T)^{\mathrm{T}}$を求める一般化固有値問題である. これを数値的に解くことを考える． $0 \leq z \leq 1$を$N$等分して$N+1$点に分ける. このとき離散点は$z_j$, $0 \leq j \leq N$となる. ここで$\Delta z=1/N$である. $W(z_j)$を$W_j$などと表すことにする。 $(D^2 W)_j$, $(D^4 W)_j$はそれぞれ \begin{align} % (D^2W)_j &=\frac{W_{j+1}-2W_j+W_{j-1}}{\Delta z^2} \\ % (D^4W)_j &=\frac{W_{j+2}-4W_{j+1}+6W_j-4W_{j-1}+W_{j-2}}{\Delta z^4} % \end{align} となる。 境界条件を離散化すると、 \begin{align} % \frac{W_{-1} - W_1}{2\Delta z} = 0, \quad \frac{W_{N+1} - W_{N-1}}{2\Delta z} = 0, % \end{align} 他の境界条件とまとめると、 \begin{align} % W_0 &= 0, \quad W_N = 0, \\ W_{-1} &= W_1, \quad W_{N+1} = W_{N-1}, \\ T_0 &= 0, \quad T_N = 0. % \end{align} 固有関数は$2(N+1)=2N+2$点， そこから境界条件から既知の要素$4$点を除くと $2N+2-4=2(N-1)$次元の行列になる．

プログラム

プラントル数 $Pr$, レイリー数 $Ra$ と波数 $a$ を与えると第一不安定モード/最小減衰モードの成長率 (以下，単に成長率と呼ぶ)と それに対応するモード(固有関数)を出力するプログラムコードを 示す(growth-rr-tt-diff.f90)．

ここで，非対称行列の一般化固有値問題を解くために Lapack の zgegv サブルーチン を用いた．

プログラムコードを少し変更し $Ra$ と $a$ について繰り返し成長率を求めるように 変更したものを示す(growth-rr-tt-diff2.f90)． これを用いれば，ベクトル画像描画ツール (asymptote) を用いることで， 「成長率」と成長率がゼロとなる「中立曲線」を求めることができる．

プログラムと描画スクリプト一覧

結果

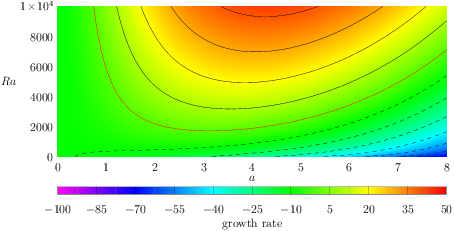
線形不安定の成長率を等値線で $a$-$Ra$ 平面にプロットしたものを示す． ここで $Pr=1$ とした． 赤実線が中立曲線，黒実線が正の成長率の等値線， 黒点線が負の成長率の等値線である． 中立曲線の下側が線形安定領域，上側が線形不安定領域である． この図を描くのに用いたデータから， $Ra \approx 1707.762$ で $a \approx 3.117$ の撹乱が もっとも低いレイリー数で線形不安定となることが分かる．

wavenumber and Rayliegh number dependence of growth rate

図は asymptote で次のコマンドにより png ファイルを生成した． asy -f png growth-rr-tt-diff2.asy として png ファイルを生成した．

参考文献

Copyright © 2014 Shin-ya Murakami [murashin _at_ gfd-dennou.org]