/地球流体セミナー
/講演資料一覧
/2003-09-08/
球面浅水系でのシア不安定
金星大気の線形安定性を調べる
伊賀 晋一(地球フロンティア)
2003 年 9 月 10 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.

|
タイトルぺージ
|

|
目次
|

|
研究の軌跡
|
|
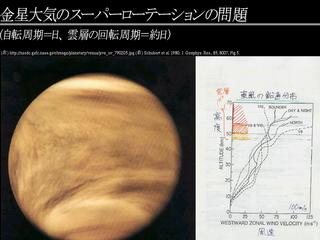
金星スーパーローテーションの問題
雲層高度で 4 日で一周する流れ
- 左 : 金星の紫外線画像.
- 右 : 探査衛星によって観測された東西風の鉛直分布.
|

|
金星スーパーローテーションの成因
|
|
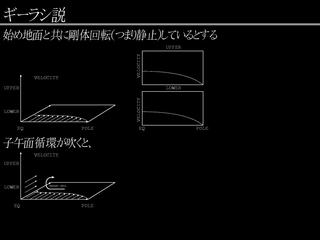
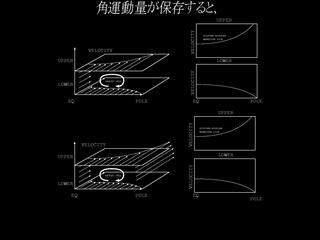
ギーラシ説
- 水平渦粘性を仮定し, それによる拡散によって角運動量を定緯度へ輸送する.
|
|
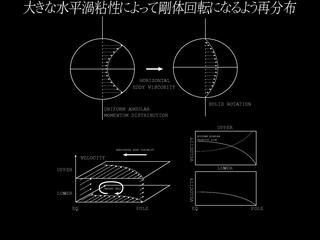
ギーラシ説(つづき)
|
|
ギーラシ説(つづき)
|

|
ギーラシ説の問題点
|

|
どのような系で考えるか ?
|

|
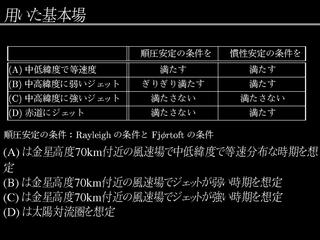
過去の球面浅水系での研究
- Dikpati and Gilman (2001) : 太陽の Tachocline を想定.
- Tachocline : 輻射層と対流層の間に存在するちょっと安定な領域.
表層の対流が貫入する.
- Tachocline の由来 : Tachocline の内側と外側で回転速度が変化するから.
内側では剛体回転, 外側は西風加速.
- 基本場の層厚は非一様.
- Boyd (1982), Dunkerton (1990) : 赤道上空のパンケーキ構造.
|

|
用いた浅水方程式系
|

|
計算の方法
|
|
用いた基本場
|
|
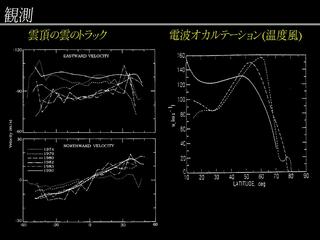
観測される風速の緯度分布
|
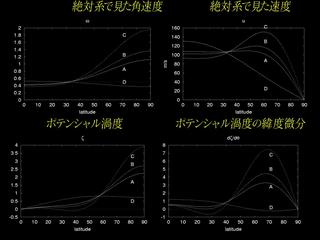
|
基本場の設定
|
|
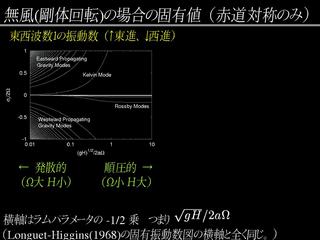
固有値問題の結果: 剛体回転の場合
|
|
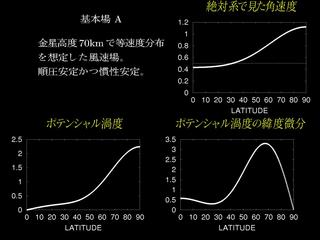
基本場 A の設定
|
|
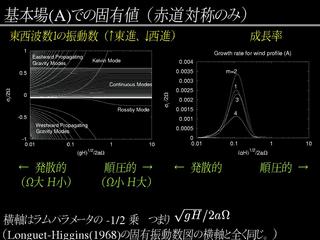
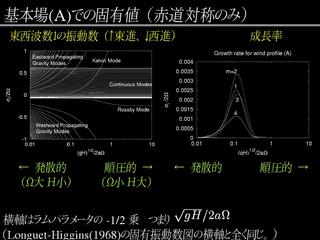
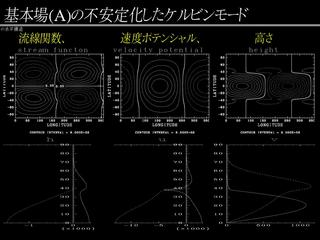
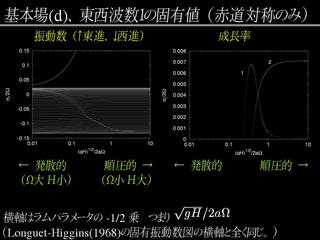
固有値問題の結果: 基本場 A の場合
- 赤道対称, 東西波数 1.
- 連続モードが現れる.
- 一部のロスビー波は連続モードと重なってよく見えない.
- 基本場の風は剛体回転に比べ, 高緯度で速く, 定緯度で遅い
- 不安定なケルビンモードが存在する.
|
|
不安定化したケルビンモードの構造
|

|
角運動量輸送の定式化
- 3 次元プリミティブ方程式系に対応する角運動量輸送を考える.
- 変数分離して, 水平構造部分を取り出す.
|
|
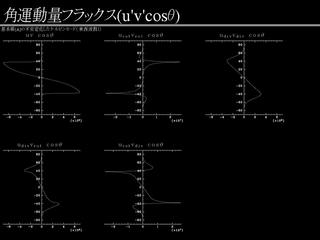
角運動量輸フラックス
不安定なケルビンモードによる角運動量輸送をみる
- 全体では赤道向きの輸送
- 赤道向き輸送に寄与するのは urotvdiv 成分
- 純粋な順圧不安定成分である urotvrot
成分は極向き輸送
|
|
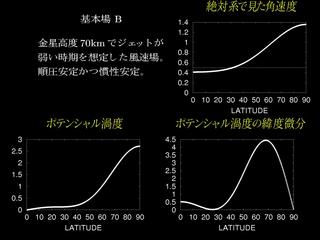
基本場 B
- 基本場 A の緯度間の速度差を強めた場合.
- 順圧不安定, 慣性不安定は起こらない条件.
|
|
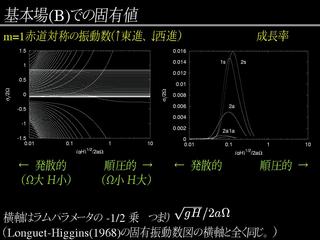
固有値問題の結果 : 基本場 B の場合
- 赤道対称, 東西波数 1.
- 左側の図の恰好は基本場 A の場合と同じ
- 不安定なケルビンモードが存在する.
|
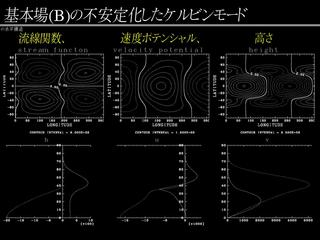
|
不安定化したケルビンモードの構造 (基本場 B)
|
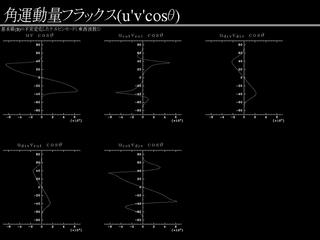
|
角運動量輸フラックス (基本場 B)
不安定なケルビンモードによる角運動量輸送をみる
- 全体では赤道向きの輸送.
- 赤道向き輸送に寄与するのは urotvdiv 成分.
- 純粋な順圧不安定成分である urotvrot
成分は極向き輸送.
|
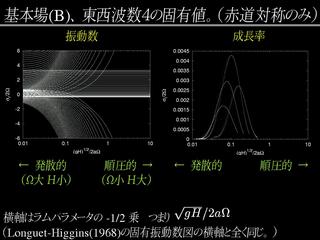
|
固有値問題の結果 : 基本場 B の場合
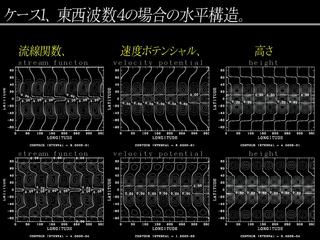
- 赤道対称, 東西波数 4.
- 西向き慣性重力波と連続モードが交差するようになる.
|
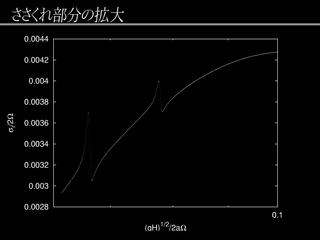
|
成長率曲線の詳細
|
|
不安定化したケルビンモードの構造 (基本場 B, 東西波数 4)
|
|
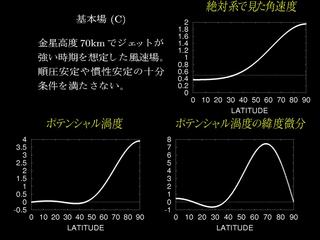
基本場 C
|
|
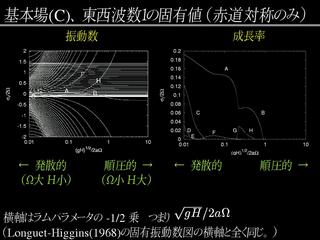
固有値問題の結果 : 基本場 C の場合
- 赤道対称, 東西波数 1.
- いろいろなモードが連続モードと重なるようになる.
- モード B はロスビーモードと同定できるか ?
|
|
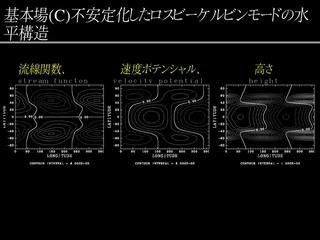
不安定なロスビー-ケルビンモードの構造 (基本場 C)
|
|
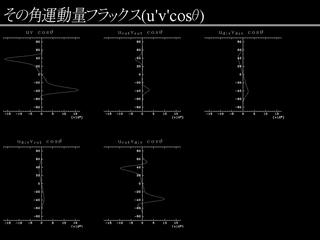
角運動量輸フラックス (基本場 C, 不安定モード A)
- 全体では赤道向きの輸送.
- 赤道向き輸送に寄与するのは urotvdiv 成分.
- 純粋な順圧不安定成分である urotvrot 成分も赤道向き輸送.
- モード B では urotvrot のみ寄与する.
|
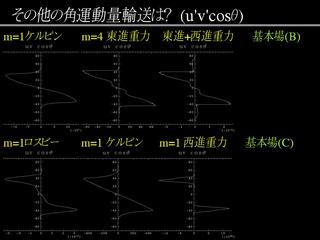
|
角運動量輸送 (その他のモード)
|

|
金星への適用
|
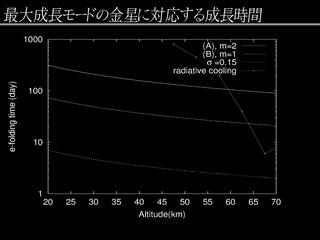
|
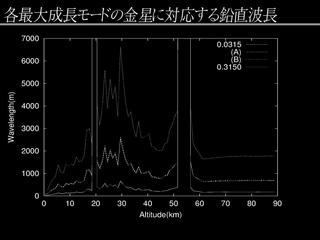
最大成長モードの成長時間
- 下から順に基本場 C, B, A.
- 成長率が高度によって異なるのは, 基本場の風速が高度とともに変化するため.
- 放射による減衰時間も示す. 上層では放射による減衰に負ける.
|
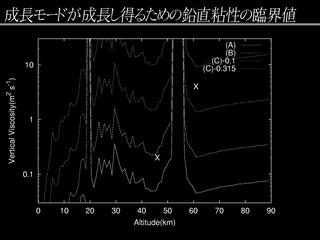
|
成長モードが成長できるための鉛直粘性の臨界値
- 実線 : 等価深度と振動数から見積もる (H2σ). 温度分布は観測値を使う.
- ×印 : 電波俺蔽観測
- Lz = 2 π / (
N2/gH -
1/4s)1/2
- H は等価深度, hs はスケールハイト
|

|
不安定モードは実際に成長できるか ?
|
|
不安定モードに対応する鉛直波長
|
|
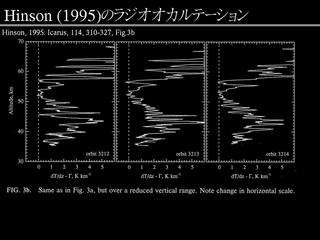
観測される温度分布
- 鉛直波長 5 km 前後の構造もある.
- 重力波, 潮汐波かもしれないが….
|

|
まとめ: 金星と球面浅水系の部分
|

|
不安定モードの成因
|

|
モードの共鳴理論
|

|
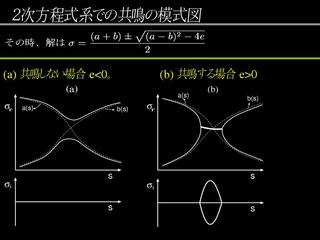
共鳴理論の理解 : 2 次方程式系で考える
|
|
2 次方程式系での共鳴の模式図
|

|
作戦
- 部分系に分割することが困難
- Hayashi and Young (1987) の方法を用いる
- 擬運動量の代わりに擬角運動量を使う
|

|
擬角運動量の定式化
- 擬運動量と同じく擬角運動量も保存量
- 共鳴する中立モードの擬角運動量は逆符号
|

|
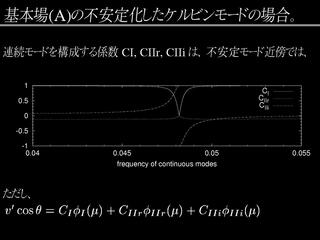
不安定モード = 連続モードとケルビンモードとの共鳴であるためには ?
|
|
連続モードの振幅
基本場 A の不安定ケルビンモードの近傍
- 振幅を φI,
φIIr,
φIIi に分割
- 係数の波数依存性
|
|
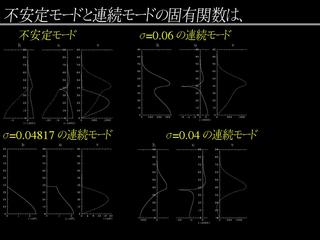
固有関数の振幅分布
- 不安定モードの実部は σ = 0.06 の連続モードに近い
- 不安定モードの虚部は σ = 0.04817 の連続モードに近い
σ = 0.04817 の連続モードを部分系のケルビンモードと考えると,
不安定モードはケルビンモードと連続モードを位相をずらして重ね合わせたものと考えられないだろうか?
|

|
擬角運動量の符号
|
|
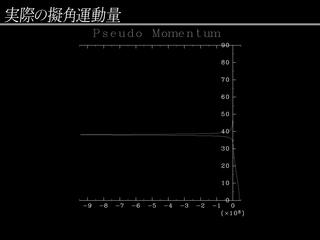
不安定ケルビンモードの擬角運動量
- 臨界緯度を挟んで項緯度側に連続モードに起因する負の領域,
低緯度側に中立なケルビンモードに起因する正の領域
|
|
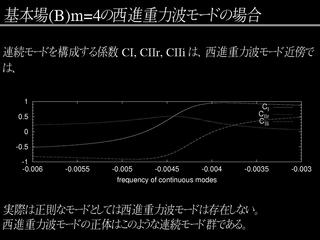
連続モードの振幅
基本場 B の m=4 西進重力波モードの近傍
|
|
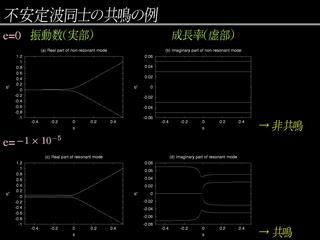
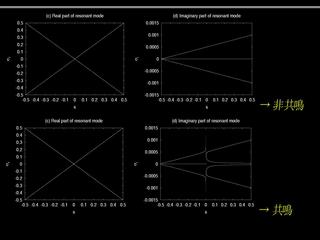
4 次方程式系モデルの振動数と成長率
- e = -1.0 × 10-5のとき,
成長率に折れ曲がりがみられる.
|

|
まとめ (モード共鳴部分)
- 球面浅水モデルで得られた不安定モードは, ケルビンモードと連続モードとの共鳴によるものであろう.
- 擬角運動量を用いると中立モードと連続モードとの共鳴による不安定が起こるか否かをある程度判定できる.
|
|
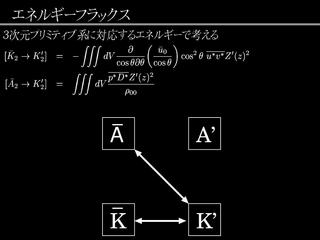
エネルギーフラックスの定式化
- 球面浅水系でのエネルギーを, 3 次元プリミティブ系と対応させて定義する.
- A' = 0 になる (単純な浅水系では h'2 が出てくる).
|
|
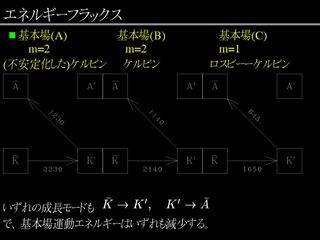
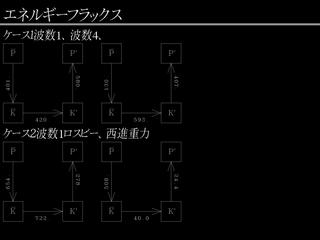
エネルギーフラックス
|
|
|

|
|

|
|
|
|
|
|
|
|
参考文献
- Balmforth, N. J., 1999: Shear instability in shallow water.
J. Fluid Mech., 387, 97-127.
- Boyd, J. P., 1982: The influence of meridional shear on planetary
waves. part I: Nonsingular wind profiles. J. Atmos. Sci.,
39, 756-769.
- Cairns, R. A., 1979: The role of negative energy waves in some
instabilities of parallel flow. J. Fluid. Mech., 92, 1-14.
- Case, K. M., 1960: Stability of inviscid plane Couette flow.
Phys. Fluids, 3, 143-148.
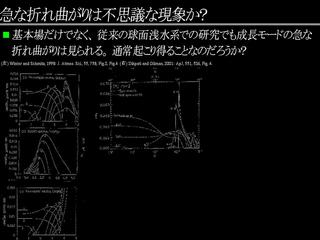
- Dikpati, M., and A. Gilman, 2001: Analysis of Hydrodynamic
stability of solar tachocline latitudinal differencial rotation
using a shallow-water model. ApJ, 551, 536-564.
- Dunkerton, J. T., 1990: Eigenfrequencies and horizontal structure
of divergent barotoropic instability originating in tropical
latitude. J. Atmos. Sci., 47, 1288-1301.
- Fels, S. B., and R. S. Lindzen, 1974: The interaction of
thermally excited gravity waves with mean flows. Gephys. Fluid
Dyn., 6, 149-192.
- Gierash, P. J., 1975: Meridional circulation and the maintenance
of the Venus atmospheric circulation. J. Atmos. Sci.,
32, 1038-144.
- Hayashi, Y.-Y. and Young, W. R., 1987:
Stable and unstable shear modes on rotating parallel flows in
shallow water, J. Fluid Mech., 184, 477-504.
- Hinson, D. P., J. M. Jenkins, 1995
Magellan radio occultation measurements of atmospheric waves on Venus.
Icarus, 114, 310-327.
- Iga, K., 1997,
Instability of a front with a layer of uniform potential vorticity,
J. Meteor. Soc. Japan, 75, 1-11.
- Iga, K., 1999a:
Critical layer instability as a resonance
between a non-singular mode and continuous modes,
Fluid Dyn. Res., 25, 63-86.
- Iga, K., 1999b,
A simple criterion for the sign of the pseudomomentum
of modes in shallow water systems,
J. Fluid Mech., 387, 343-352.
- Lin, C. C., 1961: Some mathmatical problems in the theory of the
stability of parallel flows. J. Fluid Mech., 10,
430-438.
- Longuet-Higgins, M., 1968: The eigenfunctions of laplace's tidal
equation over a sphere. Philos. Trans. Roy. Soc. London,
262, 511-607.
- Matsuda, Y., 1980:
Dynamics of the four-day circulation in the Venus atmosphere.
J. Meteorol. Soc. Japan, 58, 443-470.
- Matsuda, Y., 1982:
A further study of dynamics of the four-day circulation in the
Venus atmosphere.
J. Meteorol. Soc. Japan, 60, 245-254.
- Sakai, S., 1989:
Rossby-Kelvin instability: a new type of ageostrophic instability
caused by a resonance between Rossby waves and gravity waves,
J. Fluid Mech., 202, 149-176.
- Satomura, T., 1981: An investigation of shear onstability in a shallow water, J. Met. Soc. Japan, 59, 148-167.
- Schubert, G., A. Covey, D. Genio, L. S. Elson, G. Keating, A. Seiff,
R. E. Young, J. Apt, C. C. Counselman, III, A. J. Kriore,
S. S. Limaye, H. E. Revercomb, L. A. Sromovsky, V. E. Suomi,
F. Taylor, R. Woo, and von Zahn, U, 1980:
Structure and Circulation of the Venus Atmosphere.
J. Geophys. Res., 85, 8007-8025.
- Takagi, M. and Y. Matsuda, 1999:
Interpretation of Thompson's Mechanism for Venus' Atmospheric
Super-Rotation and its Extension to the Spherical Geometry.
J. Meteorol. Soc. Japan, 77, 971-983 .
- Thompson, R., 1970: Venus general circulation is a
merry-go-round. J. Atmos. Sci., 27, 1107-1116.
- Winter, T., and G. Schmitz, 1998: On divergent barotoropic and
inertial instability in zonal-mean flow peofiles.
J. Atmos. Sci., 55, 758-776.
- Yamamoto, M. and H. Tanaka, 1997:
Formation and maintenance of the 4-day circulation in the Venus
middle atmosphere.
J. Atmos Sci., 54, 1472-1489.
|
Odaka Masatsugu
2003-09-10
|