
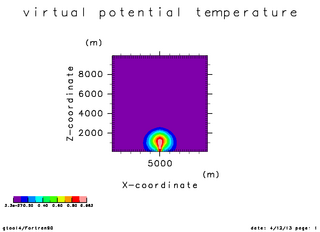
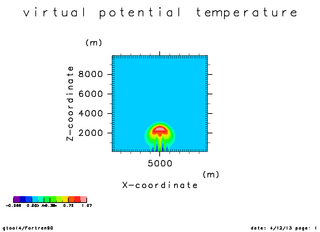
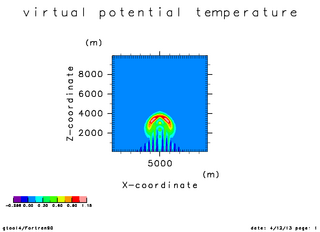
プリュームの上昇する様子を計算する. この計算では基本場は温位一様, かつ静水圧平衡としている. また粘性は無い. 地面付近においた擾乱が成長していく様子をプロットする.
| プログラムソース | arare (2004/12/12) |
| 基本場の温度 | 温位一様(300 K) |
| 基本場の圧力 | 静水圧平衡, 地表面気圧 1000 hPa |
| 音速 | 350 m/s (地表面) |
| 基本場の風速 | 0 m/s |
| 音波の減衰 | なし |
| 粘性 | なし |
| 重力 | 9.8 m/s^2 |
| 定圧比熱 | 28 J K^-1 mol^-1 |
| 分子量 | 29d-3 kg mol^-1 |
| 積分時間 | 1800 秒 |
| 計算領域 |
水平(x) : 10000 m 鉛直(z) : 10000 m |
| 境界条件 |
水平(x) : 周期境界条件 鉛直(z) : 固定境界条件 |
| 数値解法 |
水平(x) : 陽解法 鉛直(z) : 陰解法 |
| クーラン数 | 0.52 (短いタイムステップ) |
| 格子点数 | 水平(x) : 50 鉛直(z) : 50 |
| 時間間隔 |
短いタイムステップ: 0.3 秒 長いタイムステップ: 3.0 秒 (70 m/s 以上の風速で長いタイムステップに対するクーラン数が 1 を越える) |
| 出力ファイル |
VelX: arare_fs-R50_TL3_TS03.nc VelZ: arare_sf-R50_TL3_TS03.nc Exner : arare_ss-R50_TL3_TS03.nc |

|

|

|
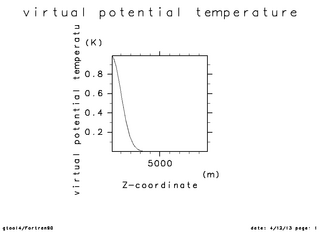
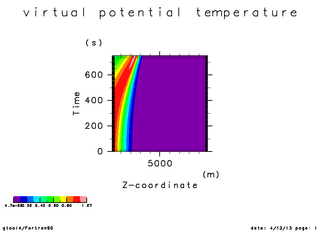
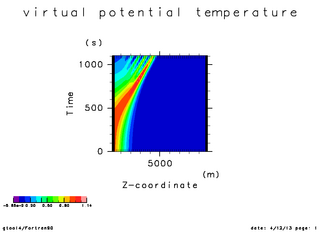
| 温位の初期振幅(x=5000 断面) | 温位の時間変化(x=5000 断面). 時刻 0 秒 -- 750 秒 | 温位の時間変化(x=5000 断面). 時刻 0 秒 -- 1100 秒 |

|

|

|
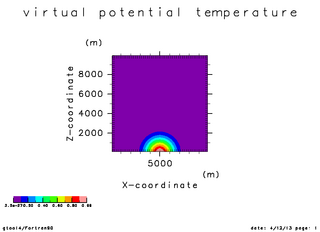
| Time = 0 秒 | Time = 250 秒 | Time = 500 秒 |

|

|
|
| Time = 750 秒 | Time = 1000 秒. 1000 秒以降は温位が乱れすぎて絵にならない. |
| クーラン数 | 0.52 (短いタイムステップ) |
| 格子点数 | 水平(x) : 50 鉛直(z) : 50 |
| 時間間隔 |
短いタイムステップ: 0.3 秒 長いタイムステップ: 6 秒 (35 m/s 以上の風速で長いタイムステップに対するクーラン数が 1 を越える) |
| 出力ファイル |
VelX: arare_fs-R50_TL6_TS03.nc VelZ: arare_sf-R50_TL6_TS03.nc Exner : arare_ss-R50_TL6_TS03.nc |
|
|
|
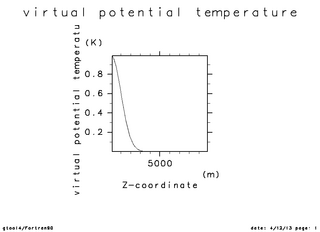
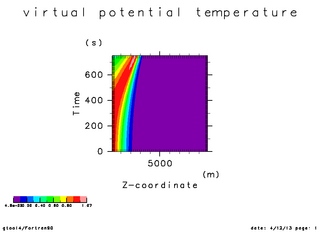
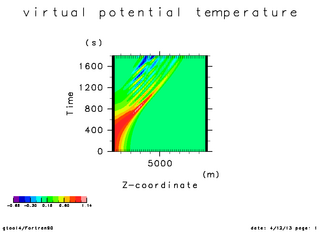
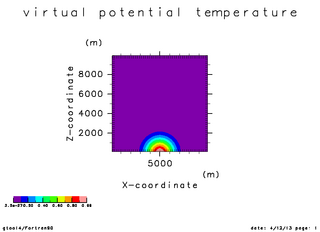
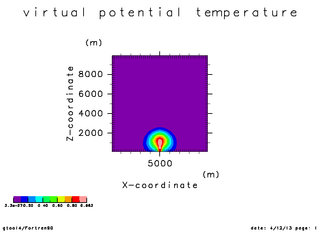
| 温位の初期振幅(x=5000 断面) | 温位の時間変化(x=5000 断面). 時刻 0 秒 -- 750 秒 | 温位の時間変化(x=5000 断面). |
|
|
|
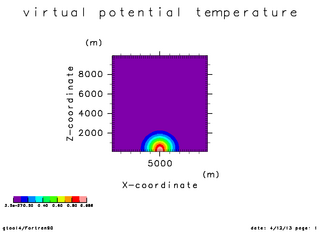
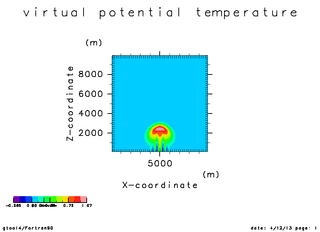
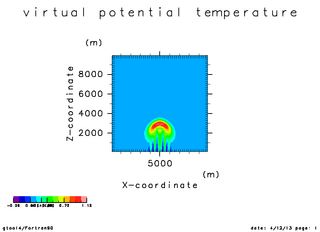
| Time = 0 秒 | Time = 250 秒 | Time = 500 秒 |
|
|
|
| Time = 750 秒 | Time = 850 秒. 850 秒以降は温位が乱れすぎて絵にならない. |
| クーラン数 | 0.52(短いタイムステップ) |
| 格子点数 | 水平(x) : 50 鉛直(z) : 50 |
| 時間間隔 |
短いタイムステップ: 0.3 秒 長いタイムステップ: 30 秒 (7m/s の流れに対して長い時間ステップのクーラン数は 1 を越える) |
| 出力ファイル |
VelX: arare_fs-R50_TL30_TS03.nc VelZ: arare_sf-R50_TL30_TS03.nc Exner : arare_ss-R50_TL30_TS03.nc |